Marching Cubes

🧊 A graphical program for exploring marching cubes + compute shaders in real-time.

Description

Marching cubes is one of the most widely used algorithms for constructing a polygonal (triangle) mesh from a scalar field. A scalar field can be thought of as a function that, for a given point in 3-space, returns a floating-point (scalar) value. Examples of scalar fields include MRI scan data, signed-distance fields, and other volumes (point clouds, etc.).

The task of marching cubes is to discretize space into a 3D grid and extract an isosurface, which is a surface containing points whose values within the scalar field are a constant (i.e. the “isolevel” - a user-specified float). In particular, each “voxel” (i.e. cell within the grid) can be in one of 256 configurations, depending on which of its 8 vertices are “inside” or “outside” the isosurface. Paul Bourke’s method (see the links below) uses a pre-computed edge table and bitwise operators to quickly compute which configuration a voxel is in. From this, we can calculate the necessary vertex information.

The algorithm readily lends itself to parallelization, as the results from any one cell are not dependent on its neighbors. Therefore, we can use GPGPU constructs (in this case, OpenGL compute shaders) to perform the isosurface extraction in real-time.

Method

The volume data is held within a 3D texture that is “animated” every frame by the first compute shader pass. By default, a (sculpted) noise field is drawn. The next compute shader pass runs the marching cubes algorithm. Specifically, it examines each cell (voxel) of the 3D volume texture and determines which (and how many) triangles to draw. The resulting triangle data (positions and normals) is written into two write-only buffers, which are subsequently used to draw a triangular mesh with a vertex + fragment shader. For now, the normals are calculated by taking the gradient of the signed-distance function (see Inigo Quilez’s website below for details).

To Use

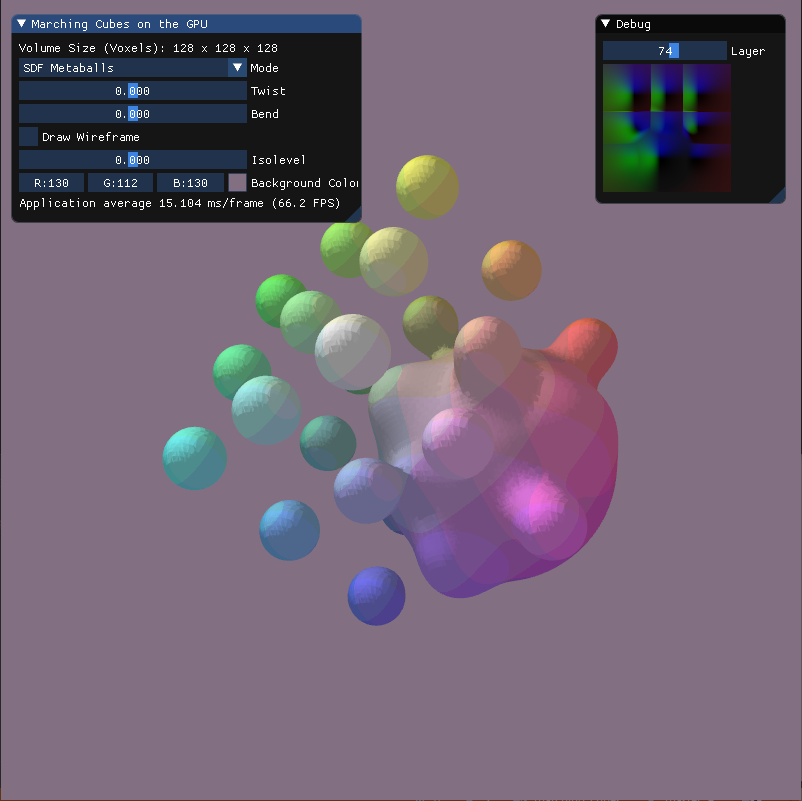
Upon launching the application, you should see two separate UI panels labeled:

• Marching Cubes on the GPU: contains controls for adjusting the isolevel, mode selection, etc.
• Debug: displays different “slices” (layers) of the 3D volume texture

You can choose between five basic modes:

• Fractal noise (default)
• Sphere
• Box
• Torus
• Metaballs

Each mode corresponds to a change in the underlying scalar field that will be used to generate triangles.

You can use your mouse to rotate the model in space. You can zoom in or out with your scroll wheel. Finally, you can “home” (i.e. reset) the current view by pressing h on your keyboard.

Credits

This project was largely inspired by and based on previous work done by Paul Bourke. Many of the functions used for the signed-distance field evaluation are taken from Inigo Quilez’s amazing website. The 3D noise function is taken from Patricio Gonzalez Vivo’s GitHub.

back