Miura-Ori

📜 A tool for generating semigeneralized Miura-ori crease patterns.

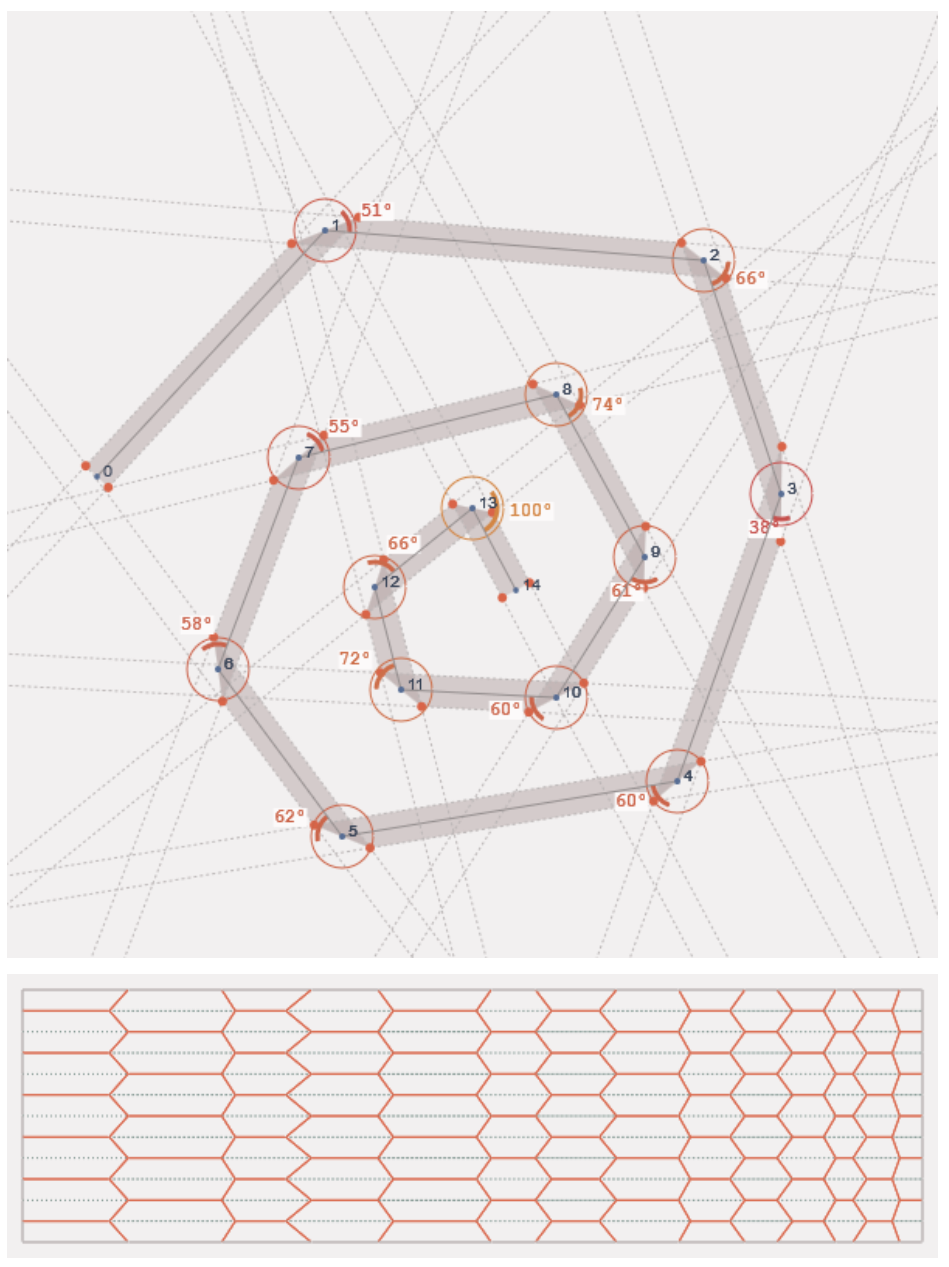
Description

Background

A drawing tool that creates Miura-ori crease patterns from an arbitrary, user-defined cross-section. You can try it out at the following URL.

Miura-ori are an interesting form of rigid origami initially discovered by Koryo Miura. They are “rigid” in the sense that they can transition smoothly from an unfolded state to a folded state without any bending or shearing of the parallelogram faces. They were even used by the Japanese space program to build deployable solar panel arrays! A “semigeneralized” Miura-ori (a term coined by Robert Lang, I believe) is a Miura-ori with an arbitrary cross-section. From Lang’s book:

A semigeneralized surface can take on any arbitrary cross section in one direction, but it exhibits strict periodicity in the other (which is the reason for the “semi” part of “semigeneralized”).

Lang, Robert J. “Twists, Tilings, and Tessellations” (p. 131)

Generating Strip

The shape of the cross-section is called the generating line for the Miura-ori. It is a piecewise-linear path in 2-dimensional space (often referred to as a “polyline” in many graphics libraries). We start by expanding the generating line along a vector orthogonal to each of the constituent line segments. This forms the generating strip, which is essentially the silhouette of the final, folded form. In order to convert this strip into a rectangular crease pattern, we have to “unwind” it as follows:

1. For each line segment of the generating line:
   1. Calculate the equations of two lines that run parallel to this line segment (the light gray dotted lines in the screenshot above): one to the “left” of the original segment, one to the “right,” where “left” + “right” are directions orthogonal to the axis of the current line segment
   2. Calculate the points of intersection (the red dots in the screenshot above) between this pair of lines and the those constructed from the previous and next line segments in the generating line (i.e. the current line segment’s “neighbors”)
   3. These four points form a closed polygon (note that any of the interior polygons generated in this step will necessarily overlap with two neighboring polygons)
2. For each of the polygons generated above:
   1. Rotate this polygon so that its bottom edge lies flat along the positive x-axis (the choice of axis here is arbitrary as long as we are consistent)
   2. Flip every other polygon: this is because “odd”-numbered polygons are rotated as the strip unfolds
3. Steps (2) and (3) create one “row” of the final crease pattern: duplicate this pattern vertically along the positive y-axis as many times as you wish, ensuring that every other “row” is flipped

Crease Assignments

The procedure outlined above generates the topology (i.e. geometric “structure”) of the crease pattern, but it doesn’t actually handle the assignment of the creases. Per Chapter 2 of Lang’s book, we will refer to creases running along the horizontal direction as minor folds and creases running along the vertical direction as major folds. Creases should be assigned as follows:

• Minor folds alternate between mountain and valley folds as we traverse the crease pattern from left to right
• Successive rows of the crease pattern start with opposite assignments (i.e. if the first row starts with a mountain fold, the next row would start with a valley fold, etc.)
• Major folds are assigned so that the surrounding vertices become “bird’s-foot” vertices (explained below)
• All edges along the border of the crease pattern are marked as “border” edges, which do not have an assignment or target fold angle

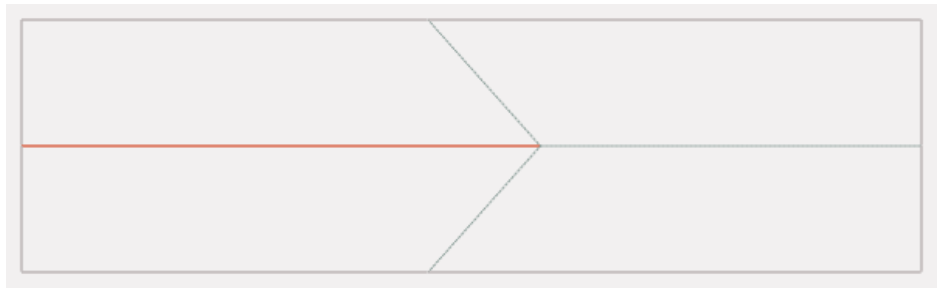
Bird’s-foot vertices are degree-4 vertices with 2 consecutive smallest sectors, where the shared crease between these two sectors is a mountain fold, and the other three creases are valley folds (or vice-versa). A single bird’s-foot vertex is show in the crease pattern below:

Export

Ultimately, the tool exports a .FOLD file, which contains a description of the vertices, edges, faces, crease assignments (mountain vs. valley fold, etc.), and target fold angles that form the resulting crease pattern. This file can then be loaded into a rigid origami simulator, such as Amanda Ghassaei’s, which simulates the folding of the crease pattern in 3D space.

To Use

Use your mouse to add points in the upper canvas. The points will be connected to form a polyline, which, in turn, will be used to generate the Miura-ori crease pattern (displayed in the lower canvas). Additional controls:

• Press the clear button to clear the current path
• Press the save button to export the crease pattern as a .FOLD file
• Adjust the repetitions slider to change the number of times that the crease pattern is repeated vertically (this corresponds to the “width” of your paper, while the horizontal axis corresponds to the “length”)

Credits

This project was largely inspired by Robert Lang’s book, Twists, Tilings, and Tessellations, which outlines the theoretical / mathematical implications of semigeneralized Miura-ori crease patterns (see Chapter 2). The .FOLD file format is maintained by Erik Demaine and colleagues.

back