Unfold

📦 A program for unfolding arbitrary convex objects.

Description

“Unfold” is an implementation of the paper Unfolding Polyhedra Method for Design of Origami Structures with Creased Folds, as described in the book Active Origami. The input to the program is a 3D model (in the form of an .obj file), and the output is a rendered image of the unfolded mesh. The resulting pattern often exhibits complex structure, but the algorithm to find such an unfolding is actually quite simple. The goal of this algorithm is to find a net (i.e. an unfolding where no faces overlap) for the given convex polyhedron.

First, we construct a spanning tree of the faces of the input mesh (also known as the goal mesh). By definition, the spanning tree touches each face of the goal mesh exactly once. To construct a spanning tree, we pick an arbitrary reference face. We add each of the reference face’s neighbors to a queue. While the queue is not empty, we pop off the last face, add it to the spanning tree, and push each of its unvisited neighbors onto the queue. We continue in this fashion until all faces have been added to the tree. The edges of the mesh that are not crossed by the spanning tree form the cut boundary. These are the edges that must be “cut” in order to unfold the mesh.

The faces of the goal mesh are rotated and translated into their positions in the net via a series of transformations:

1. Rotate each face to align its unit normal vector with the positive z-axis (“up” in our coordinate system)
2. Translate and rotate each face to place one of its vertices at the origin and one of its edges along the positive x-axis
3. Translate and rotate each face in the xy-plane to its final position in the net

All of these operations (including the calculation of the spanning tree) require extensive knowledge of how the vertices, edges, and faces of the goal mesh are connected to one another. To facilitate this, the mesh is stored as a half-edge data structure, which makes such adjacency queries fairly easy. There is a lot of existing literature on half-edge data structures, but essentially, each edge of the mesh stores a pair of directed half-edges. Every face stores a pointer to one of its half-edges. Every half-edge stores a pointer to its originating vertex, its face, the next half-edge, the previous half-edge, and its pair half-edge. Every vertex stores a pointer to one of its incident half-edges.

Limitations

Determining whether every convex polyhedra has a net is still an unsolved problem (known as “Dürer’s conjecture”). However, many non-convex polyhedra do not admit a net. Practically speaking, this means that one or more pairs of faces will overlap in the unfolded net. This greatly limits the number of shapes we can “correctly” unfold using the algorithm outlined above. For example, a torus cannot be unwrapped using this method. Nonetheless, there are still many interesting designs we can produce.

To Use

The program is meant to be used as a commandline tool. Running the executable with --help will print instructions on usage:

Unfold 0.1
Michael Walczyk
📦 A program for unfolding arbitrary convex objects.

USAGE:
    unfold.exe [FLAGS] [OPTIONS] <INPUT>

ARGS:
    <INPUT>    Sets the input .obj file, i.e. the goal mesh

FLAGS:
    -w, --wireframe    Sets the draw mode to wireframe (instead of filled)
    -h, --help         Prints help information
    -V, --version      Prints version information

OPTIONS:
    -c, --color_palette <COLOR_PALETTE>
            Sets the color palette based on the contents of the provided .json file

    -r, --resolution <PIXELS>
            Sets the resolution (width and height) of the renderer [default: 1024]

The only required parameter is the path to the .obj file that you wish to unfold. As mentioned above, the output resolution can be set with the -r flag. The canvas will always be square. By default, it is set to 1024 x 1024.

A color palette can be provided in the form of a .json file with the following schema:

{
  "background":[
    1.0,
    1.0,
    1.0
  ],
  "polygons":[
    [
      1.0,
      0.0, 
      0.0
    ],
    [
      0.0,
      1.0,
      0.0
    ],
    [
      0.0,
      0.0,
      1.0
    ]
  ]
}

In particular, background specifies the background color of the canvas. polygons is a list of one or more colors that will be cycled through when drawing the faces of the net. All of these values should be sub-lists with 3 elements (RGB) in the range 0..1. Currently, there is no way to change “how” the colors are cycled through - this is something that I would like to add in the future.

An example run (with all of the options) might look like:

unfold path/to/goal_mesh.obj -c path/to/color_palette.json -w -r 1280

After some computation, the application should launch a window displaying the final net. You can take a screenshot of this window using any standard screenshot utility that is part of your operating system. I’d like to have a button or small menu to do this, but for now, I’ve left it as-is (mostly because there isn’t a good way to take screenshots in Bevy yet - the library I’m using for rendering).

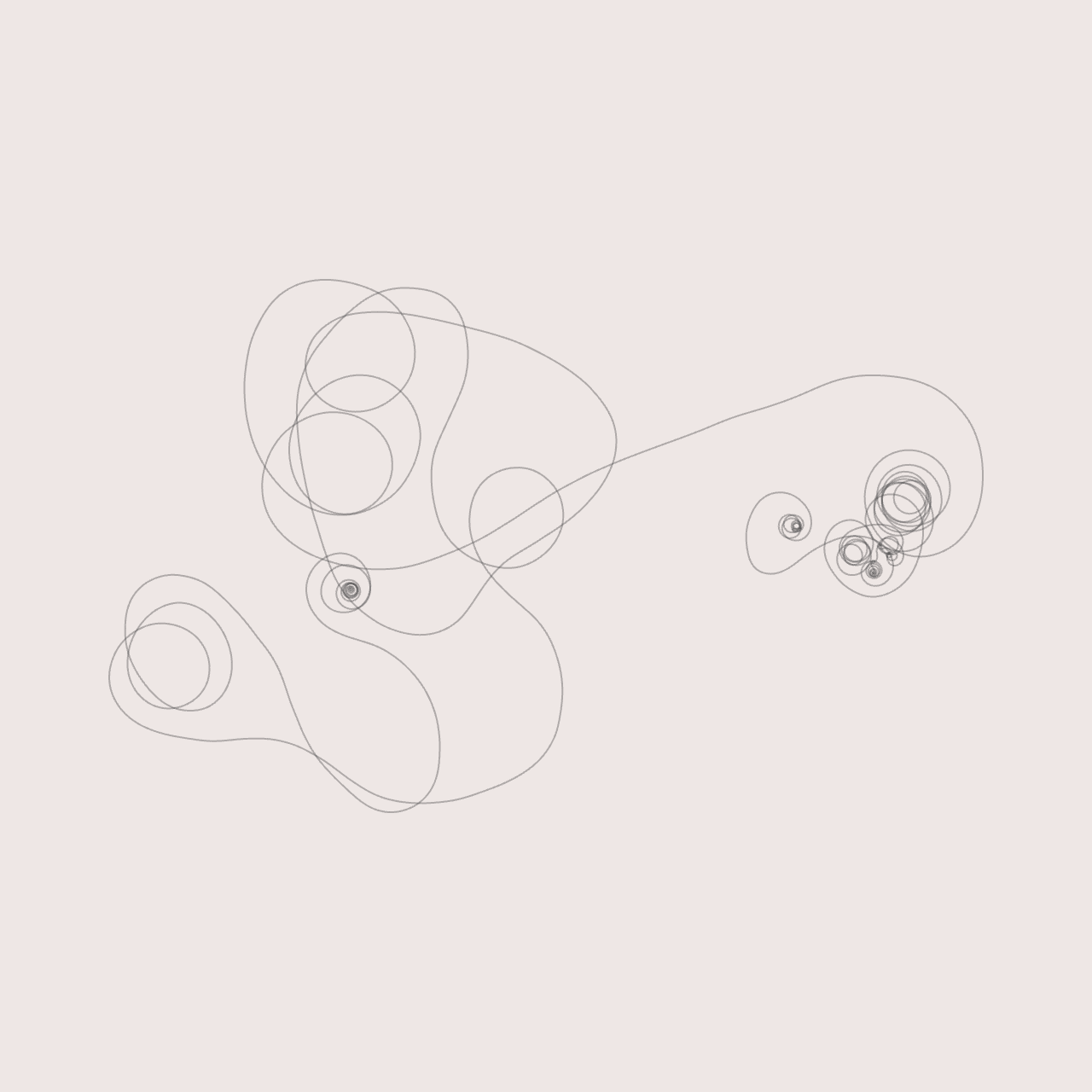
The rendered images featured on this page come from various convex shapes I’ve modeled and manipulated in Blender. I found a lot of interesting results by sorting the faces of the .obj file before processing. For example, sorting all faces based on the y-coordinate of their centroids (Blender has built in commands for doing this). This affects the order in which faces are added to the spanning tree and thus, the look and feel of the final design.

Future Directions

Eventually, I would like to make the software “headless,” so that it simply writes an .svg file without relying on a windowing system and/or OpenGL / Vulkan. This would make it easier to send the final net to a plotter or cutting / scoring machine.

There are, of course, more advanced algorithms that are able to handle non-convex objects. I am most interested in Tomohiro Tachi and Erik Demaine’s “tuck-folding” method for origami design, which can handle pretty much any goal mesh. This algorithm is implemented in their software Origamizer.

Credits

The methodology outlined in this repo was largely based on (and inspired by) the book Active Origami. If you are interested in the intersection of origami, engineering, and material science, I highly recommend you check out this book! The main difference between my implementation and the one described in the book is the use of the half-edge data structure for adjacency queries.

The platonic solids in the goal_meshes folder are from the following repository.

I learned how to make custom iterators in Rust from @nical’s own half-edge implementation here, which greatly simplified a lot of my code.

back